SIR感染症モデル

 コロナウイルスについていろいろな感染症モデルがあるようです。以前から言語伝搬モデルに似てるかもと思ってました。一番単純とされるSIRモデルについてですが、

『パンデミックを阻止せよ！』、浦島充佳、DOJIN選書084、株式会社化学同人
という本をまねしてやってみました。

まずS：Susceptibleで免疫を持たず感染発症する可能性のある人
I：Infectiousで感染性を有する人、次の段階でRになる。
R：Resistantで感染から回復し免疫を持つ。再度感染しない人。
単純化しているので、いろいろな仮定があります。

初期状態はS=N（全体人数）で1000人とします。感染者I=1、回復した人R=0です。
感染はIとRの接触で起こり、I*Rに比例すると考えます。たとえばS=3で、I=2ならば接触回数は３＊２＝６となり回数に比例して感染すると考えています（と思う）。勘違いしてるかもしれませんので信用しないでください。

本では微分方程式で表されていますが、要はSは感染者が出た分減り、感染者は次の段階で、Rに変化し、どんどん増えていくというモデルです。どれだけ感染者が出るかは、その一つ前の段階のSとRによります。

サンプルの計算では、その人数Iは、keisuu＊S＊R/1000です。keisuuは本では1.8でしたが、2.0に変えてみました。この分がSから減っていきます。

後のS＝前のSー前のI、後のI＝前の段階のSとRで計算、後のR＝前のR＋前のI

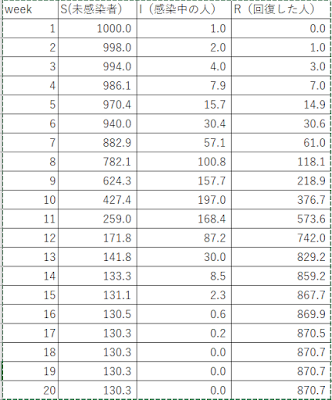
これで作ったエクセルの表を示します。縦に時間の経緯を示します。

これをグラフにしました。横軸が時間の経過です。

全員が感染するかと、最初予想しましたが、そうではなく、Sの人数は一定の値から減らず、130人ぐらいの下限があります。つまりこの段階で集団免疫を持ったということだろうと思います。これは感染していない人も周りの免疫を持った人に守られ感染が抑えられたということを示しているようです（多分）。

言語伝搬のモデルにどうあてはまるかわかりませんが、いろいろ応用が利きそうなモデルには思います。流行語もある程度の広がりで落ち着くのかもとかこのモデルでいけるかもとか思います。高齢者でデジタル機器を使いこなせないので講習をするとかのニュースがありましたが、これなどもデジタル感染症に影響を受けない人がある程度存在するということなのかもしれません。